Craps Dice Probability Explained: Why 7 Appears More Often Than Other Numbers

This article is part of our complete guide on How Craps Really Works: Dice Probability, Bets, and Why Myths Persist, which explains craps probability, house edge, variance, and why common myths fail.
Dice Probability Is About Combinations, Not Totals
Craps is governed by a simple mechanical truth: two dice create combinations, not equal totals.
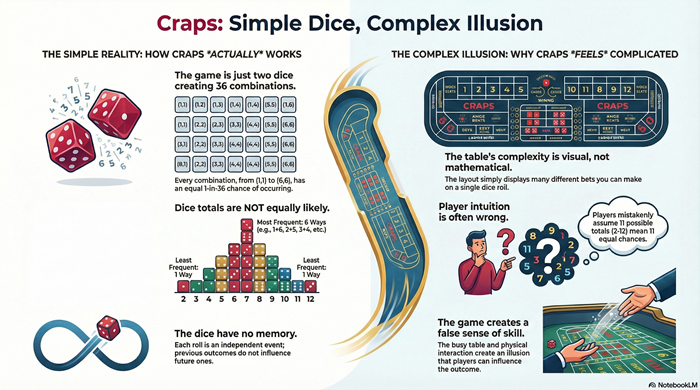
Players experience the game through totals—2 through 12—but the dice themselves produce ordered pairs. Each roll results in one of 36 equally likely combinations, and probability flows directly from how many combinations produce a given total.
This distinction is critical. Most confusion about craps odds begins by ignoring it.
The Full Distribution of Two-Dice Outcomes
All 36 Outcomes Are Equally Likely
When two fair six-sided dice are rolled, each die has six faces and each face is equally likely.
That means:
- There are 36 possible ordered combinations
- Each combination occurs with probability 1 in 36
- (1,6) and (6,1) are different outcomes
Order matters for probability, even if the total is the same.
How Many Ways Each Total Can Occur
Totals appear at different rates because they can be formed in different numbers of ways.
- 2 → 1 way
- 3 → 2 ways
- 4 → 3 ways
- 5 → 4 ways
- 6 → 5 ways
- 7 → 6 ways
- 8 → 5 ways
- 9 → 4 ways
- 10 → 3 ways
- 11 → 2 ways
- 12 → 1 way
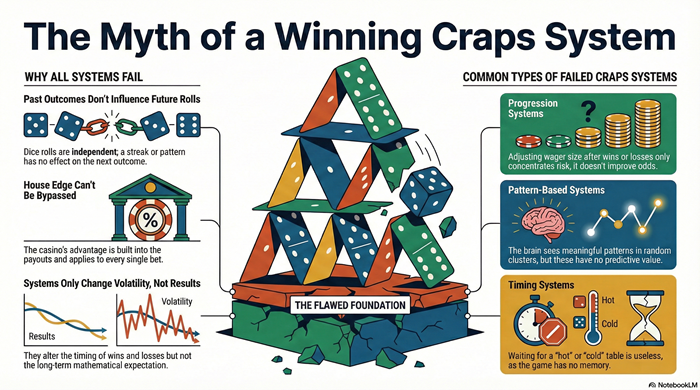
This distribution is fixed. It cannot change during play.
Why 7 Appears More Often Than Any Other Number
The Mathematical Reason
The total 7 can be formed in six distinct ways:
- (1,6)
- (2,5)
- (3,4)
- (4,3)
- (5,2)
- (6,1)
No other total has more than five combinations.
As a result, 7 has a probability of 6/36 (1/6) on every roll. Totals like 2 and 12 occur only 1/36 of the time.
This imbalance is the structural center of the game.
Why This Feels Counterintuitive
Many players assume that because there are 11 totals, each one should appear roughly equally.
Dice do not work that way. Totals are labels. Combinations are reality.
The brain notices outcomes, not the combinatorial paths that produce them.
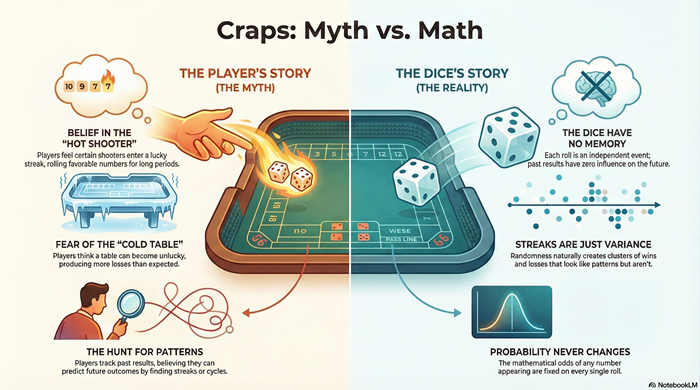
Frequency Does Not Mean Predictability
Common Misinterpretations
Because 7 appears more often, players often conclude that:
- it is “due” after a long absence
- it is “unlikely” after appearing repeatedly
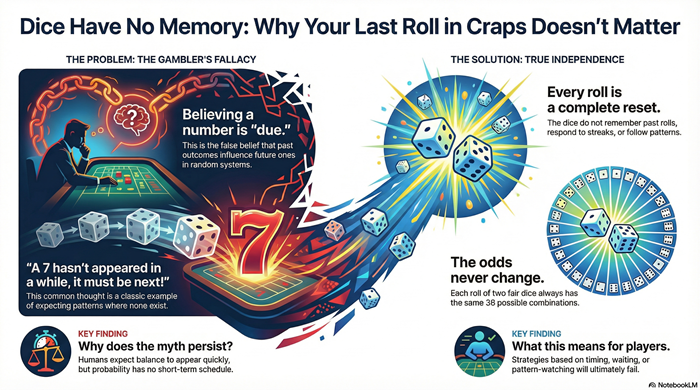
Both conclusions are wrong.
Frequency describes long-run distribution, not short-run behavior.
Independence Still Applies
Even though 7 has the highest probability, each roll is independent.
The probability of rolling a 7 is always 1/6, regardless of what happened before.
Six rolls without a 7 do not increase the chance of a 7 next time. Three 7s in a row do not reduce it.
The Shape of the Distribution Matters
Why Extremes Are Rare
Totals near the edges—2, 3, 11, and 12—are rare because very few combinations produce them.
Small changes in dice faces push results toward the center of the distribution.
This creates a pyramid-shaped probability curve, narrow at the edges and wide in the middle.
Why This Shapes Player Experience
Because the distribution is uneven:
- some numbers feel “active”
- others feel dramatic when they appear
- long gaps for rare totals are normal
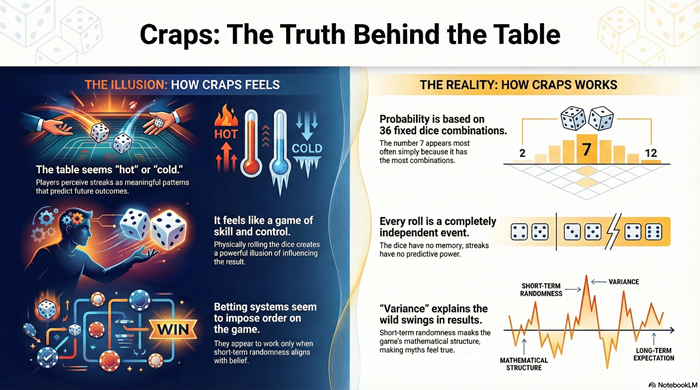
Players often mistake normal distribution behavior for meaningful signals.
Probability vs Short-Term Results
Why Sessions Feel Erratic
In the short run:
- rare numbers can appear quickly
- common numbers can temporarily disappear
- streaks cluster naturally
This volatility does not contradict probability. It is an expected feature of it.
Where Myths Begin
When players expect smooth alternation or quick balance, they misinterpret randomness as:
- hot tables
- cold tables
- changing conditions
The math never changed. Expectations did.
What This Means for Understanding Craps
Craps probability is not hidden or negotiable.
It is fixed, mechanical, and determined entirely by two dice.
Understanding this distribution explains why some numbers dominate the game, why others feel special, and why intuition so often conflicts with reality.
Related Pages
- How Craps Really Works: Dice Probability, Bets, and Why Myths Persist
- What Is Craps? Dice Mechanics, Outcomes, and Why the Table Looks So Complicated
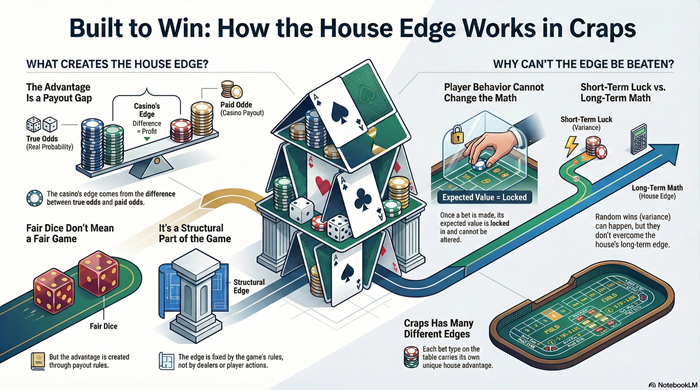
- House Edge in Craps: How the Casino Advantage Is Built Into the Game
- Variance in Craps: Why Results Swing Wildly Even When Odds Are Fixed
- Myths About Craps That Refuse to Die