What Are the Odds in Keno? Understanding Spot Selection and True Winning Probability
This article is part of our complete guide on How Keno Really Works: Probability, Payouts, and Why “Almost Winning” Feels So Close, which explains keno probability, house edge, variance, and why common myths fail.
Introduction
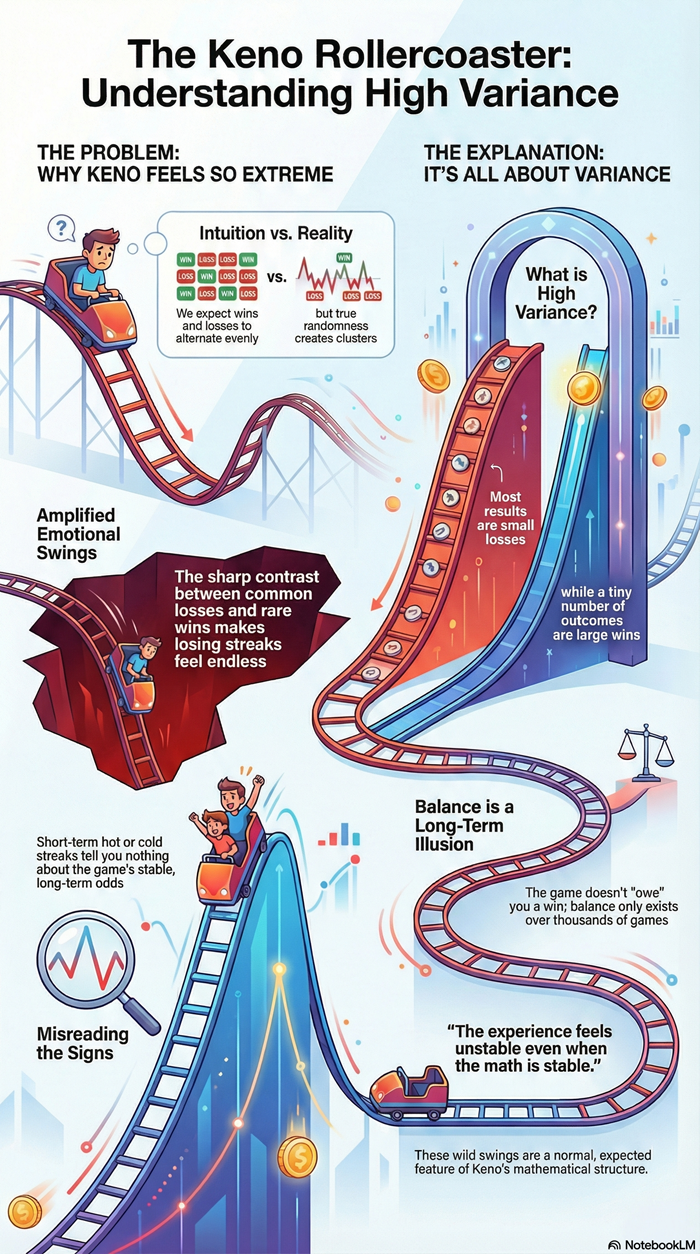
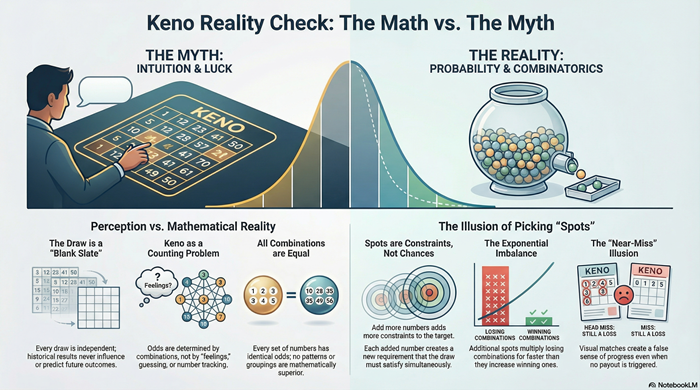
Keno odds are often described vaguely, using phrases like “long shots” or “low chances,” without explaining why those chances behave the way they do. To understand keno honestly, the odds must be examined as a counting problem, not as a feeling or a guessing exercise.
At its core, keno is governed by combinatorics: the mathematics of combinations. Once that framework is clear, many common beliefs about picking more numbers, being “close,” or improving chances stop making sense.
What Are the Odds in Keno? Understanding Spot Selection and True Winning Probability
How Keno Draws Actually Work
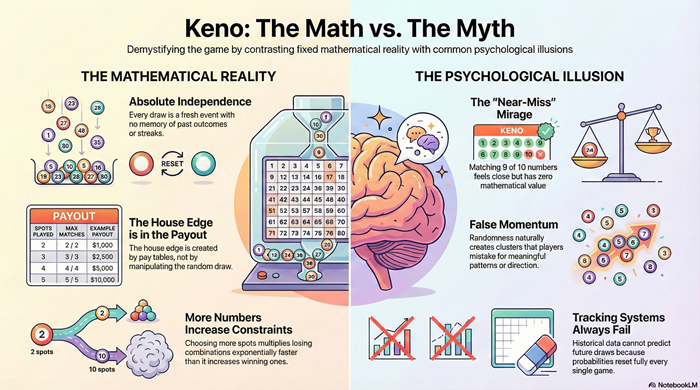
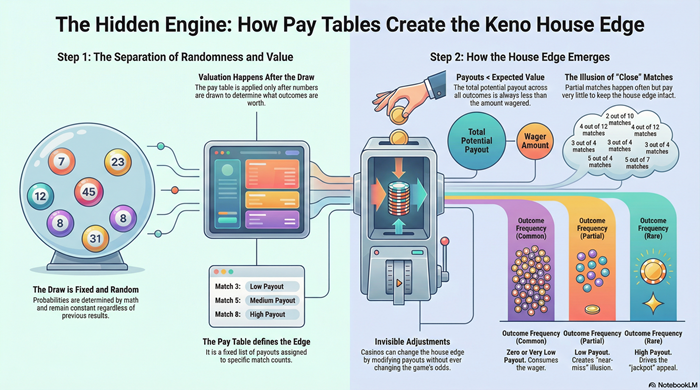
A keno game begins with a fixed pool of numbers. From that pool, a fixed number of balls are drawn at random. Every possible draw has the same chance of occurring. No number is favored, avoided, or adjusted based on history.
This matters because the draw itself never changes. The odds are not influenced by which numbers you choose, how often you play, or what happened in previous rounds. Every ticket is evaluated against the same random process.
Once the draw occurs, the outcome is fully determined. There are no secondary stages, adjustments, or corrections. The mathematics of the game begin and end with that single random selection.
What “Picking Spots” Really Means
In keno, a “spot” refers to how many numbers you select on a ticket. Choosing four numbers is called a four-spot. Choosing ten numbers is a ten-spot. This choice feels flexible, but mathematically it is decisive.
When you select your spots, you are not increasing opportunities. You are defining how many exact matches are required for different outcomes to occur. Each additional spot adds another condition that must be met simultaneously.
This is where intuition often fails. People tend to think of spot selection as expanding coverage. In reality, it narrows the set of winning outcomes by increasing the number of requirements the draw must satisfy at once.
The Mathematics Behind Keno Odds
Keno odds come from counting how many different ways a draw can occur compared to how many of those ways count as wins for your ticket.
The total number of possible draw combinations is extremely large. The number of combinations that match all of your chosen numbers is extremely small. As spot count increases, the total number of possible combinations grows rapidly, while the number of exact-match combinations grows very slowly.
This imbalance is not gradual. It is exponential. Each additional number multiplies the number of losing combinations far more than it increases winning ones.
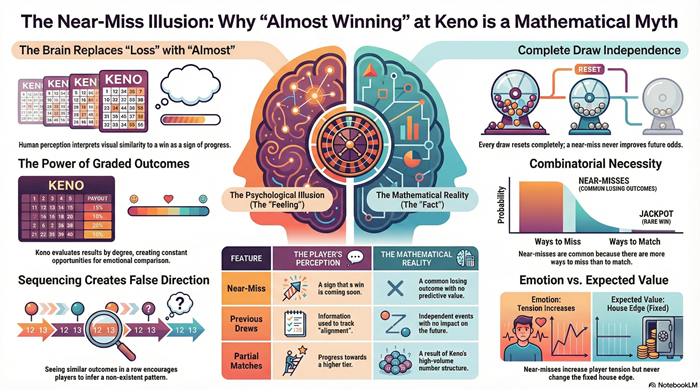
Partial matches do not change this reality. Missing one number is still missing the exact condition required for a top outcome. There are far more near-miss combinations than exact matches, which is why near-misses are common and wins are rare.
Why More Spots Feel Better but Perform Worse
Choosing more numbers produces more visible matches. Seeing several of your numbers appear in the draw feels like progress, even when it results in no meaningful payout.
This visual feedback creates a false sense of effectiveness. The ticket looks active. Numbers light up. Results appear close. But none of that improves the underlying probability.
From a mathematical perspective, higher-spot tickets introduce more ways to fail. They feel engaging because they generate more partial results, not because they generate better odds.
The increase in perceived activity masks the decline in true success probability. This is why keno can feel exciting while remaining unforgiving.
Common Misunderstandings About Keno Odds
One common belief is that choosing more numbers gives “more chances.” In reality, it gives more constraints.
Another belief is that being close matters. Missing by one number feels different than missing by several, but mathematically both outcomes are equally unsuccessful for higher-tier payouts.
A third misunderstanding is that some number selections are easier than others. In keno, every combination of the same size has identical odds. There are no favorable numbers, patterns, or groupings.
These misunderstandings persist because the game provides frequent feedback without providing context.
What This Means for Understanding Keno (Not Playing It)
Understanding keno odds requires abandoning the idea of incremental improvement. There is no warm-up, no momentum, and no advantage gained from prior outcomes.
Spot selection defines the probability structure of your ticket immediately. From that point forward, every draw simply applies that structure to a random result.
Once odds are understood this way, later concepts—such as pay tables, house edge, variance, and near-miss effects—become easier to place correctly. Keno stops feeling unpredictable for mysterious reasons and starts behaving like a rigid counting problem that produces uneven experiences by design.