European vs American Roulette: Odds, Zeros, and the Cost of an Extra Pocket

This article is part of our complete guide on How Roulette Really Works: Odds, House Edge, and Why Systems Fail, which explains roulette odds, house edge, wheel types, and why betting systems fail.
Why This Comparison Actually Matters
At first glance, European and American roulette appear nearly identical. The table layout looks familiar. The bets have the same names. The payouts are the same. Many players assume the difference is cosmetic or trivial.
Mathematically, it is neither.
The distinction between these two wheels is one of the clearest examples in gambling of how small structural changes create large long-term consequences. Understanding this difference is essential for grasping how house edge works, why roulette outcomes feel misleading, and why betting systems collapse under scrutiny.
This is not about strategy or preference. It is about geometry, probability, and expectation.
Roulette Wheels Are Probability Machines
Roulette is not defined by its bets. It is defined by its number of possible outcomes.
Every spin results in the ball landing in exactly one pocket. The probability of each outcome is determined solely by how many pockets exist on the wheel. Payouts, however, are fixed and do not adjust when pockets are added.
This mismatch is where the house edge lives.
European Roulette: One Zero, 37 Outcomes
Wheel Structure
- Numbers: 1 through 36
- Additional pocket: single zero (0)
- Total outcomes: 37
Probability Basics
Each individual number has a probability of:
1 ÷ 37 ≈ 2.70%
All bets—inside and outside—are priced as though there are only 36 outcomes, not 37. That missing probability is the casino’s advantage.
House Edge
- 2.70% on all standard bets
This means that over a very large number of spins, the expected loss is €2.70 for every €100 wagered, regardless of how those bets are placed.
American Roulette: One Extra Pocket, 38 Outcomes
Wheel Structure
- Numbers: 1 through 36
- Additional pockets: single zero (0) and double zero (00)
- Total outcomes: 38
Probability Basics
Each individual number has a probability of:
1 ÷ 38 ≈ 2.63%
The extra zero increases the number of losing outcomes without increasing payouts.
House Edge
- 5.26% on all standard bets
This is nearly double the cost of European roulette, created entirely by a single additional pocket.
Side-by-Side Mathematical Comparison
Total Outcomes
- European roulette: 37
- American roulette: 38
House Edge
- European roulette: 2.70%
- American roulette: 5.26%
Long-Term Expectation
If two players wager identical amounts over time:
- The European roulette player loses about half as much, on average
- Neither player has a winning expectation
This difference persists regardless of session length, betting pattern, or perceived streaks.
Why Payouts Stay the Same
Roulette payouts were standardized centuries ago based on a 36-number wheel. When casinos introduced additional zero pockets, they did not rebalance payouts to maintain fairness.
Consider a straight-up bet:
- Pays 35 to 1
- Fair payout with 37 outcomes would be 36 to 1
- Fair payout with 38 outcomes would be 37 to 1
That gap between fair payout and actual payout is the house edge. Every added zero widens it.
The same logic applies to all bets, including red/black, odd/even, dozens, and columns.
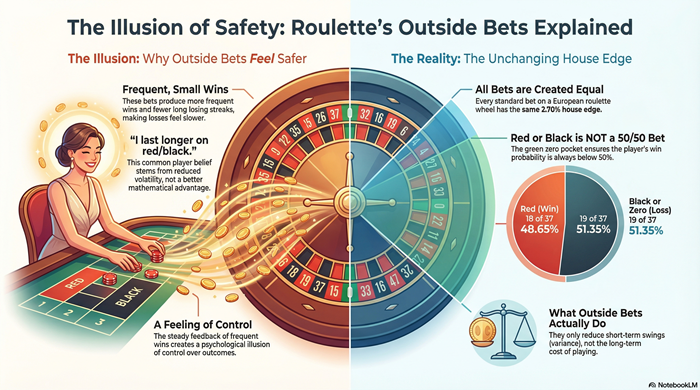
Outside Bets Do Not Escape the Math
A common misconception is that European roulette is “safer” because outside bets feel more stable. This is a psychological effect, not a mathematical one.
Example: Red/Black
- European roulette: 18 red, 18 black, 1 zero
- Win probability: 18 ÷ 37 ≈ 48.65%
- Loss probability: 19 ÷ 37 ≈ 51.35%
Despite nearly even outcomes, the zero ensures the expected value remains negative.
On American roulette, the two zero pockets push that imbalance even further.
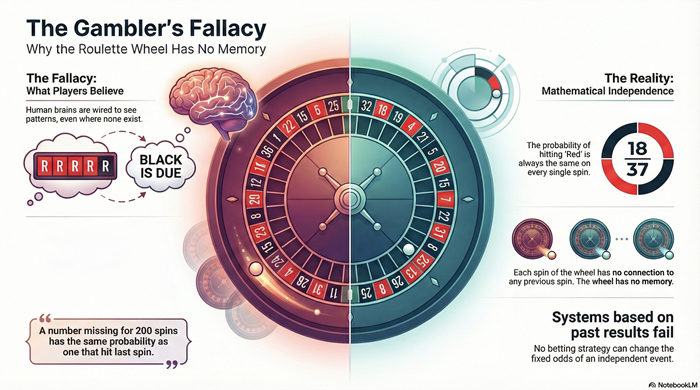
Independence Does Not Change Between Wheels
European roulette has a lower house edge, but the independence of spins remains absolute:
- Previous spins do not affect future spins
- Zeros do not become “due”
- Switching wheels does not reset probability
- Streaks do not change expectation
The wheel does not remember outcomes. Only the player does.
Why Systems Fail on Both Wheels
Many betting systems rely on:
- Progression
- Pattern recognition
- Betting “around” zeros
- Waiting for deviations
None of these alter the number of pockets on the wheel.
The European wheel simply loses money more slowly. The American wheel loses money faster. Neither can be turned into a positive-expectation game.
Systems fail not because players choose the wrong bets, but because the structure of the game is fixed.
What This Comparison Teaches About Roulette
European roulette is objectively less expensive than American roulette. That is a factual, mathematical statement.
What it is not:
- A winning game
- A solvable system
- A predictable process
This distinction explains why roulette feels fair in the short term but is uncompromising in the long term. The wheel design determines the outcome distribution. Everything else is interpretation layered on top.
Understanding this difference is a foundation for understanding why roulette systems fail, regardless of confidence, discipline, or experience.
Related Articles in This Roulette Series